+91-8527521718
Signup | Login
  • 1(current)
Q. No.
The radiation emerging from a furnace (blackbody) is found to have a most probable wavelength \(\lambda_m\) and the gas molecules (air) emerging from it have an RMS speed \(v.\) As the temperature of the furnace is varied:
1. \(\lambda_m\propto v \) 2. \(\lambda_m\propto \dfrac1v \)
3. \(\lambda_m\propto v^2 \) 4. \(\lambda_m\propto \dfrac1{v^2} \)
Subtopic:  Wien's Displacement Law |
 65%
From NCERT

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

When radiant energy from a blackbody at temperature \(T,\) is analysed, and the most probable wavelength of the radiation is \(\lambda_{\text{mp}},\) then:
1. \(\lambda_{\text{mp}}\propto T\)
2. \(\lambda_{\text{mp}}\propto \Large\frac1T\)
3. \(\lambda_{\text{mp}}\propto T^{1/2}\)
4. \(\lambda_{\text{mp}}\propto T^{\text-1/2}\)
Subtopic:  Wien's Displacement Law |
 79%
From NCERT

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

Gas molecules at a temperature \(T\) are enclosed within a thin-walled enclosure, the inner and outer walls having the same temperature \(T\) in equilibrium. The rms speed of the gas molecules is \(v_{\text{rms}}.\) The enclosure radiates outward as a blackbody, and the most probable wavelength is \(\lambda_{\text{mp}},\) in the blackbody radiation. As the temperature of the gas varies, so do \(v_{\text{rms}}\) and \(\lambda_{\text{mp}}.\) The relationship between \(v_{\text{rms}}\) and \(\lambda_{\text{mp}}\) is:
1. \(\lambda_{\text{mp}}v_{\text{rms}}=\text{constant}\)    2. \(\Large\frac{\lambda_{\text{mp}}}{v_{\text{rms}}}\)\(=\text{constant}\)   
3. \(\lambda_{\text{mp}}v^2_{\text{rms}}=\text{constant}\) 4. \(\Large\frac{\lambda_{\text{mp}}}{v^2_{\text{rms}}}\)\(=\text{constant}\)
Subtopic:  Wien's Displacement Law |
 64%
From NCERT

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

advertisementadvertisement
The value of Wien's constant, \(b\) is \(3\times10^{-3}~\text{m-K}.\) The cosmic background radiation can be considered to be equivalent to a blackbody radiation at \(3~\text K.\) The most probable wavelength in this radiation is:
1. \(1~\text{mm}\)
2. \(1~\text{m}\)
3. \(10^3~\text{m}\)
4. \(1~\mu\text{m}\)
Subtopic:  Wien's Displacement Law |
 80%
From NCERT

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

The maximum intensity of emission occurs at a wavelength of \(1~\mu \text{m}\) in the spectrum of radiation emitted by a star. Take Wien's constant as \(3~\text{mm}\text-\text{K}.\) The surface temperature of the star is (nearly):
1. \(1000~\text K\) 2. \(3000~\text K\)
3. \(1000^\circ\text C\) 4. \(3000^\circ\text C\)
Subtopic:  Wien's Displacement Law |
 88%
From NCERT

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

Radiant light from three different stars \(A,B,C\) arriving on the Earth is analysed by a prism and the intensities \((I)\) are plotted as a function of wavelength \((\lambda).\) If the absolute temperatures of the stars are \(\theta_A,\theta_B,\theta_C\) then:
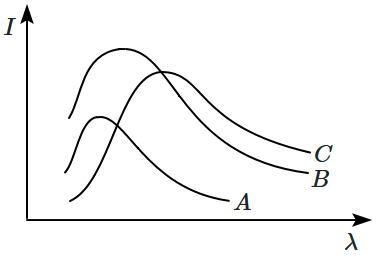
1. \(\theta_B>\theta_A=\theta_C\)
2. \(\theta_A>\theta_B>\theta_C\)
3. \(\theta_C>\theta_B>\theta_A\)
4. \(\theta_B<\theta_A=\theta_C\)
Subtopic:  Wien's Displacement Law |
 68%
From NCERT

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

advertisementadvertisement
Given below are two statements:
Statement I: If the absolute surface temperature of a star doubles, the most probable wavelength in the radiation spectrum also doubles.
Statement II: If the absolute surface temperature of a star doubles, the rate of radiant energy loss from the star increases to \(16\) times its initial value.
 
1. Statement I is incorrect and Statement II is correct.
2. Both Statement I and Statement II are correct.
3. Both Statement I and Statement II are incorrect.
4. Statement I is correct and Statement II is incorrect.
Subtopic:  Wien's Displacement Law |
 73%
From NCERT

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

The radiant emission spectrum from a blackbody shows a peak at a wavelength of \(3~\mu\text m.\) The temperature of the blackbody is nearly: 
(take Wien's constant \(=3~\text{mm}\cdot\text{K}\)):
1. \(1000^\circ\text C\) 2. \(1000~\text K\)
3. \(10000~\text K\) 4. \(10^5~\text K\)
Subtopic:  Wien's Displacement Law |
 86%
From NCERT

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

  • 1(current)
Q. No.

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions

© 2025 GoodEd Technologies Pvt. Ltd.