Unlock IMPORTANT QUESTION
This question was bookmarked by 5 NEET 2025 toppers during their NEETprep journey. Get Target Batch to see this question.
✨ Perfect for quick revision & accuracy boost
Buy Target Batch
Access all premium questions instantly
Plane waves of light of wavelength \(\lambda\) are incident onto a convex lens, and the beam is brought to a focus. A plane slab of thickness \(t\) having refractive indices \(\mu_1,~\mu_2\) in the upper and lower halves is placed parallel to the incoming wavefronts. The phase difference between the wavefronts at the focus, coming from the upper and lower halves of the slab is:


| 1. | \(\dfrac{2 \pi}{\lambda}\left[\left(\mu_{1}-1\right) t+\left(\mu_{2}-1\right) t\right]\) |
| 2. | \(\dfrac{2 \pi}{\lambda}\left(\mu_{1}-\mu_{2}\right) t\) |
| 3. | \(\dfrac{2 \pi}{\lambda}\left(\dfrac{t}{\mu_{1}}-\dfrac{t}{\mu_{2}}\right)\) |
| 4. | \(\dfrac{2 \pi}{\lambda}\left(\dfrac{t}{\mu_{1}}+\dfrac{t}{\mu_{2}}\right)\) |
Subtopic: Huygens' Principle |
Level 3: 35%-60%

To unlock all the explanations of this course, you need to be enrolled.
Hints

To unlock all the explanations of this course, you need to be enrolled.
Unlock IMPORTANT QUESTION
This question was bookmarked by 5 NEET 2025 toppers during their NEETprep journey. Get Target Batch to see this question.
✨ Perfect for quick revision & accuracy boost
Buy Target Batch
Access all premium questions instantly
Sound waves travel faster in water than in air. Imagine a plane sound wavefront incident at an angle \(\alpha\) at the air-water interface; the refracted wavefront making an angle \(\beta\) with the interface. Then,


| 1. | \(\alpha>\beta\) |
| 2. | \(\beta>\alpha\) |
| 3. | \(\alpha=\beta\) |
| 4. | the relation between \(\alpha~\&~\beta \) cannot be predicted. |
Subtopic: Huygens' Principle |
Level 3: 35%-60%

To unlock all the explanations of this course, you need to be enrolled.
Hints

To unlock all the explanations of this course, you need to be enrolled.
A light beam traveling along the \(x\text-\)axis with a planar wavefront is incident on a medium of thickness \(t\). In the region, where light is falling, the refractive index can be taken to be varying such that \(\dfrac{dn}{dy}>0.\) The light beam on the other side of the medium will emerge:
1. parallel to the \(x\text-\)axis
2. bending downward
3. bending upward
4. split into two or more beams
1. parallel to the \(x\text-\)axis
2. bending downward
3. bending upward
4. split into two or more beams
Subtopic: Huygens' Principle |
Level 3: 35%-60%

To unlock all the explanations of this course, you need to be enrolled.
Hints

To unlock all the explanations of this course, you need to be enrolled.
Match Column-I with Column-II.
Choose the correct option from the given ones:
| Column-I | Column-II | ||
| \(\mathrm{(A)}\) | Light diverging from a point source | \(\mathrm{(P)}\) | plane wavefront |
| \(\mathrm{(B)}\) | Light emerging from a convex lens when a point source is placed at its focus | \(\mathrm{(Q)}\) | spherical wavefront |
| \(\mathrm{(C)}\) | Light reflected from a concave mirror when a point source is placed at its focus | \(\mathrm{(R)}\) | cylindrical wavefront |
| \(\mathrm{(D)}\) | 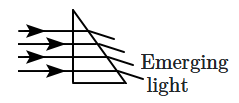 |
\(\mathrm{(S)}\) | concave right wavefront |
Choose the correct option from the given ones:
| \(\mathrm{A}\) | \(\mathrm{B}\) | \(\mathrm{C}\) | \(\mathrm{D}\) | |
| 1. | \(\mathrm{(Q)}\) | \(\mathrm{(R)}\) | \(\mathrm{(P)}\) | \(\mathrm{(S)}\) |
| 2. | \(\mathrm{(R)}\) | \(\mathrm{(P)}\) | \(\mathrm{(S)}\) | \(\mathrm{(Q)}\) |
| 3. | \(\mathrm{(P)}\) | \(\mathrm{(S)}\) | \(\mathrm{(Q)}\) | \(\mathrm{(R)}\) |
| 4. | \(\mathrm{(Q)}\) | \(\mathrm{(P)}\) | \(\mathrm{(P)}\) | \(\mathrm{(P)}\) |
Subtopic: Huygens' Principle |
75%
Level 2: 60%+

To unlock all the explanations of this course, you need to be enrolled.
Hints

To unlock all the explanations of this course, you need to be enrolled.


